Design Of Crane Hook Formulas
Crane Hook Blueprint Optimization
Design a crane hook to conduct a load F. The hook has a rectangular cross section with width b (minimum 0.2 mm) and height h.
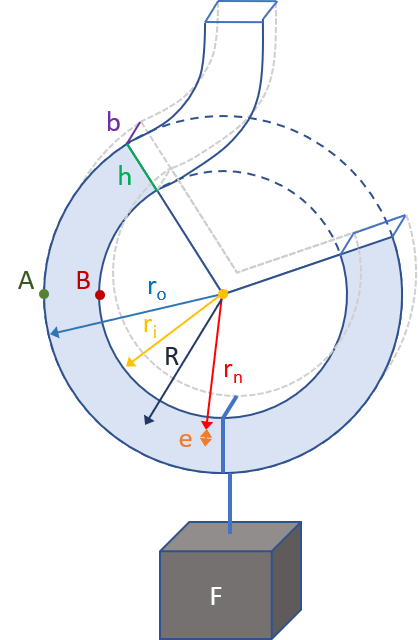
Optimize the crane hook pattern to minimize the volume of the hook. The claw is manufactured from a complete rectangular wire ring that is clipped and bent to give the final claw shape. The outer radius of the hook is ro and the inner radius is ri with a minimum inner diameter of 3.0 mm. The height is the difference between the outer and inner radius h=ro-ri . The bending moment is M=F R with a strength F of 100 N (ten.2 kg for a static load on globe). The centroid radius is R and the neutral axis radius is rn .
$$r_n = \frac{h}{\ln\left(r_o/r_i\correct)}$$
The difference betwixt the centroid radius and the neutral axis radius is e. The stress at betoken A is
$$\sigma_A = \frac{M \left(r_o-r_n\right)}{b\;h\;e\;r_o}$$
The stress at signal B is
$$\sigma_B = \frac{Grand \left(r_n-r_i\right)}{b\;h\;e\;r_i}$$
The stress at points A and B should not exceed the yield strength of the steel at 430 Northward/mm2 .
Solution
# Crane Claw optimization
from gekko import GEKKO
from numpy import pi
m = GEKKO(remote= Faux )
# Constants
F = 100 # load (N)
S_y = 430 # yield force of steel (North/mm^2)
# Form D fine-carbon steel (ASTM A255)
# Variables
r_o= m.Var ( )# outer radius (mm)
r_i= thou.Var (lb= one.5 )# inner radius (mm)
b= g.Var (lb= 0.2 )# hook width (mm)
V= grand.Var ( )# hook volume (mm^3)
# Intermediates
h= r_o - r_i# hook height (mm)
R= (r_o + r_i)/ii# radius of the centroid (mm)
r_n= h/chiliad.log (r_o/r_i) # radius of the neutral axis (mm)
e= R - r_n# R - r_n (mm)
G= F * R# bending moment due to the load
c_o= r_o - r_n# distance from outer to neutral(mm)
c_i= r_n - r_i# distance from inner to neutral(mm)
Area = b*h# cross-exclusive expanse (mm^2)
o_A = (M*c_o/(Expanse*e*r_o) ) # outer stress
o_B = (M*c_i/(Area*e*r_i) ) # inner stress
# Equations
m.Equations ( [
Five == pi*(r_o**2-r_i**2 )*b, # volume calculation
o_A < S_y,# yield stress @ A < yield forcefulness
o_B < S_y,# yield stress @ B < yield strength
r_i < r_o # constraint for feasibility
] )
# Objective
m.Minimize (Five)
# Solve
thousand.options.SOLVER = three
m.solve ( )
print ( 'Optimal Volume: ' + str (V[ 0 ] ) )
print ( 'Optimal outer radius: ' + str (r_o[ 0 ] ) )
print ( 'Optimal inner radius: ' + str (r_i[ 0 ] ) )
print ( 'Optimal claw width: ' + str (b[ 0 ] ) )
The optimal solution is:
Optimal Volume: 37.fifty mm^2 Optimal outer radius: 3.39 mm Optimal inner radius: 1.l mm Optimal hook width: 1.29 mm
Design Of Crane Hook Formulas,
Source: https://apmonitor.com/me575/index.php/Main/CraneHook
Posted by: johansenunly1998.blogspot.com


0 Response to "Design Of Crane Hook Formulas"
Post a Comment